
Okam je pozni sholastički mislilac koga mnogi smatraju osnivačem nominalizma, škole koja zastupa tezu da univerzalije nisu odvojena stvarnost od pojedinačnih stvari koje su označene univerzalnim ili opštim pojmom. Upamćen je i kao pokretač srednjovekovnog pravila logičke ekonomije poznate pod nazivom Okamova oštrica.
Rođen je 1285. godine u Okamu, Sari. Bio je engleski franjevac, filozof, teolog i politički mislilac. Još dok je bio veoma mlad pridružio se franjevcima, kod kojih je stekao početno obrazovanje, a zatim je otišao na Oksfordski univerzitet. Studije nije završio, ali je tokom studija i neposredno nakon njih napisao većinu filozofskih i teoloških dela po kojima je postao poznat. Okam je pozni sholastički mislilac koga mnogi smatraju osnivačem nominalizma, škole koja zastupa tezu da univerzalije nisu odvojena stvarnost od pojedinačnih stvari koje su označene univerzalnim ili opštim pojmom. Upamćen je i kao pokretač srednjovekovnog pravila logičke ekonomije poznate pod nazivom Okamova oštrica. Mnogi ga smatraju jednim od najvećih logičara svih vremena. Kao franjevac, Okam je posvetio svoj život krajnjem siromaštvu, a papa Jovan XXII ekskomunicirao ga je zbog odbrane franjevačkog zaveta siromaštva i zalaganja za prava carstva u odnosu na papstvo. Umro je 1349. godine u Minhenu, Bavarska.
Okamova oštrica (Occam’s razor)
Metodološki princip štedljivosti u naučnom objašnjenju koji se tradicionalno pripisuje Vilijamu od Okama. Taj princip propisuje da entiteti ne treba da se ponavljaju više od neophodnog. U praksi to podrazumeva da ako se pojava može objasniti bez dovođenja u sumnju postojanja samog identiteta, onda to znači da naučnici i filozofi taj identitet ne bi trebalo ni da proveravaju.
Po tom principu, objašnjenje bilo kojeg fenomena treba da ima što je moguće manje pretpostavki, eliminišući one koje ne utiču na zaključke hipoteze ili teorije. Taj princip se često izražava izrekom Entia non sunt multiplicanda praeter necessitatem („Entiteti se ne smeju umnožavati više nego što je potrebno”). Druga varijanta te izreke glasi Pluralitas non est ponenda sine necessitate („Umnožavanje ne treba pretpostavljati ako za to nema potrebe”). Obe rečenice tačno predstavljaju suštinu Okamove filozofije, ali do sada nisu pronađene ni u jednom od njegovih radova. Naime, one su zapisane od strane drugih autora, tek posle Okamove smrti. Najpribližnija verzija koja je pronađena u njegovim delima jeste Numquam ponenda est pluralitas sine necessitate („Nikad ne treba pretpostavljati umnožavanje ako za to nema potrebe”). Okamova oštrica se vrlo često parafrazira na sledeći način: „Ako su svi ostali kriterijumi jednaki, najjednostavnije rešenje obično je najbolje rešenje.” Drugim rečima, kad je više različitih teorija ili objašnjenja jednako u svim ostalim pogledima, treba izabrati ono rešenje koje uvodi najmanje pretpostavki i postulira najmanje entiteta. Dakle, treba napraviti „oštar rez” između najjednostavnijeg i svih ostalih rešenja, i odbaciti ona koja nepotrebno komplikuju stvar.
Poreklo onoga što je postalo poznato kao Okamova oštrica može se naći u delima ranijih filozofa kao što su Mejmonajdis (1138–1204), Toma Akvinski (1225–1274), pa čak i Aristotel (384–322. pre n. e.). Izraz „Okamova oštrica” prvi put se pojavio 1852. godine, u delima škotskog metafizičara ser Vilijama Hamiltona (1788–1856), vekovima posle Okamove smrti. Okam nije izmislio „oštricu”, tako da njeno povezivanje sa njim može biti zbog toga što ju je često i efikasno koristio.
Grafička interpretacija
Treba povući liniju kroz četiri tačke u koordinatnom sistemu (slika 1). To može da bude prava linija (slika 2), ali i bilo koja druga linija (slike 3. i 4, još dva moguća rešenja, pri čemu postoji neograničen broj mogućih rešenja). Ipak, logično je da se kao najjednostavnije izabere prvo rešenje, a odbace sva ostala.
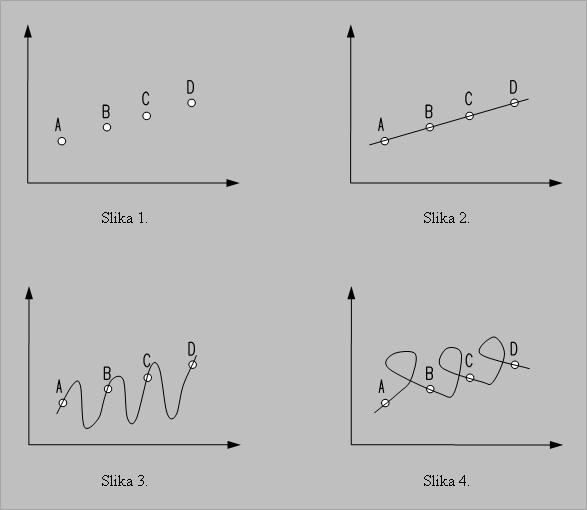
Iz Okamove oštrice izveden je i stav koji je definisao američki astronom i astrobiolog Karl Segan (1934–1996): „Posebna tvrdnja zahteva poseban dokaz.” Taj stav se može ilustrovati istim grafičkim primerom – ako se, na primer, opredelimo za rešenje sa slike 3, tu odluku moramo da obrazložimo, tj. da objasnimo zašto smo izabrali baš to rešenje. Samo prvo rešenje (slika 2) ne zahteva posebno objašnjenje, jer ni rešenje ni po čemu nije posebno.
Opšte obrazovanje

